EXPRESSION TREE
เป็นการนำเอาโครงสร้างทรีไปใช้เก็บนิพจน์ทางคณิตศาสตร์โดยเป็นไบนารีทรี ซึ่งตและโหนดเก็บ Operator และ Operand ของนิพจน์คณิตศาสตร์ไว้ หรืออาจจะเก็บค่านิพจน์ทางตรรกะ เมื่อแทนนิพจน์ต่างลงในทรีต้องคำนึงถึงลำดับขั้นตอนในการคำนวณตามความสำคัญของเครื่องหมายด้วย โดยมีความสำคัญ คือ ฟังก์ชัน วงเล็บ ยกกำลัง เครื่องหมายหน้าเลขจำนวน(unary) คูณหรือหาร บวกหรือลบ ตามลำดับ และถ้ามีเครื่องหมายที่ระดับเดียวกันให้ทำจากซ้ายไปขวา
ในการแทนนิพจน์ใน expression tree นั้น operand จะเก็บอยู่ที่โหนดใบ ส่วน operator จะเก็บในโหนดกิ่ง หรือโหนดที่ไม่ใช่โหนดใบ
BINARY SEARCH TREE
เป็นไบนารีทรีที่ค่าของโหนดรากมีค่ามากกว่าค่าของทุกโหนดในทรีย่อยทางซ้าย และมีค่าน้อยกว่าหรือเท่ากับค่าของทุกโหนดในทรีย่อยทางขวาและในแต่ละทรีย่อยก็จะมีคุณสมบัติเช่นเดียวกัน
ปฏิบัติการเพิ่มโหนดหรือดึงโหนดออกจาก Binary Search Tree ค่อนข้างยุ่งยาก เนื่องจากหลังปฏิบัติการเสร็จเรียบร้อยแล้วต้องคำนึงถึงความเป็น Binary Search Tree ของทรีนั้นด้วย ซึ่งสามารถทำได้ดังนี้
1. การเพิ่มโหนด ถ้าทรีว่างโหนดที่เพิ่มเข้าไปก็จะเป็นโหนดรากของทรี แต่ถ้าทรีไม่ว่างต้องทำการตรวจสอบก่อนว่าโหนดใหม่ที่เพิ่มเข้าไปมีค่ามากกว่าหรือน้อยกว่าโหนดราก ให้เปรียบเทียบตามคุณสมบัติที่กล่าวไว้ข้างต้น
2. การดึงโหนดออก ซึ่งหลังจากที่ดึงออกแล้วนั้นต้องคงความเป็น Binary Search Tree ไว้ ก่อนที่จะทำการดึงโหนดต้องค้นหาก่อนว่าโหนดที่ต้องการจะดึงออกอยู่ที่ตำแหน่งไหนภายในทรี สามารถพิจารณาได้เป็น 3 กรณีคือ
ก.) กรณี่เป็นโหนดใบ สามารถดึงออกได้เลยทันที โดยให้ค่าในลิงค์ฟิลด์ของโหนดแม่ซึ่งเก็บที่อยู่ของโหนดที่ต้องการดึงออกให้มีค่าเป็น Null
ข.) กรณีที่มีเฉพาะทรีย่อยทางซ้ายหรือทรีย่อยทางขวาเพียงด้านใดด้านหนึ่ง โดยใช้วิธีเดียวกับการดึงโหนดออกจากลิงค์ลิสต์ โดยให้โหนดแม่ของโหนดที่จะดึงออกชี้ไปยังโหนดลูกของโหนดนั้นแทน
ค.) กรณีที่มีทั้งทรีย่อยทางซ้ายและทางขวาต้องเลือกโหนดมาแทนโหนดที่ถูกดึงออก โดยถ้าโหนดที่มาแทนที่เป็นหนดที่เลือกจากทรีย่อยทางซ้ายต้องเลือกโหนดที่มีค่ามากที่สุดในทรีย่อยทางซ้ายนั้น แต่ถ้าเลือกโหนดจากทรีย่อยทางขวาต้องเลือกโหนดที่มีค่าน้อยที่สุดในทรีย่อยทางขวานั้น
GRAPH
เป็นโครงสร้างข้อมูลที่มีโครงสร้างประกอบไปด้วยโหนด (Vertixes) และการเชื่อมต่อ(Edges) ลักษณะการเชื่อมต่อจะแตกต่างจากโครงสร้างข้อมูลแบบอื่น ๆ คือ สามารถที่จะเชื่อมต่อแต่ละโหนดได้หลากหลาย และทิศทางของการเดินทางสามารถเชื่อมต่อได้หลากหลายเช่นกัน มีความสัมพันธ์ได้ทั้ง 2 แบบ คือ แบบไม่ระบุทิศทาง และแบบระบุทิศทาง ดังภาพ
การเขียนกราฟแสดงโหนดและเส้นเชื่อมความสัมพันธ์ระหว่างโหนดไม่มีรูปแบบที่ตายตัว การลากเส้นความสัมพันธ์เป็นลักษณะใดก็ได้ที่สามารถแสดงความสัมพันธ์ระหว่างโหนดได้ถูกต้อง นอกจากนี้ เอ็จโหนดใด ๆ สามารถวนเข้าหาตัวมันเองได้
การจัดเก็บกราฟด้วยวิธีการเก็บโหนดและพอยน์เตอร์ยุ่งยากในการจัดการเพิ่มขึ้น เนืองจากต้องเก็บโหนดและพอยน์เตอร์ในแถวลำดับ 2 มิติ และต้องจัดเก็บโหนดที่สัมพันธ์ด้วยในแถวลำดับ 1 มิติ และควรใช้ในกราฟที่ไม่มีการเปลี่ยนแปลงตลอดการใช้งาน
กราฟที่มีการเปลี่ยนแปลงตลอดเวลา ควรใช้วิธี Adjacency List ซึ่งเป็นวิธีที่คล้ายวิธีการจัดเก็บกราฟแบบการเก็บโหนดและพอยน์เตอร์ แต่แตกต่างกันตรงที่จะใช้ลิงค์ลิสต์แทน เพื่อความสะดวกในการเปลี่ยนแปลงแก้ไข มีหลักคือ
- การแทนค่าแต่ละแถวของอะเรย์ 2 มิติจะกลายเป็นลิงค์ลิสต์
- หัวแถวจะเป็นโหนดของกราฟ จะมีเท่ากับจำนวนโหนด
- โหนดในแต่ละแถวคือ โหนดที่อยู่ข้างเคียงหรือเพื่อนบ้านของโหนดหัวแถว
ตัวอย่างเช่น
การแทนที่กราฟด้วยเมทริกซ์ หรือ Adjacency Matrix เป็นโครงสร้างที่ประกอบไปด้วยโหนดและเส้นเชื่อมต่อที่บอกถึงเส้นทางของการเดินทาง หรือความสัมพันธ์ในทิศทางซึ่งสามารถนำมาแทนความสัมพันธ์นั้นด้วยการกำหนดเมตริกซ์ n x nตัวอย่างเช่น
สามารแทนที่กราฟแบบเมทริกซ์ได้ดังนี้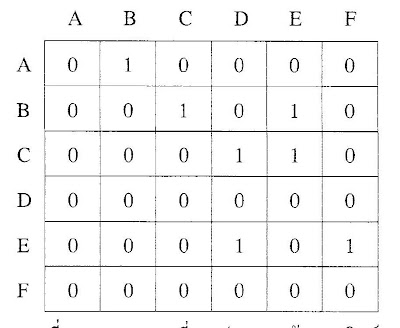
จากภาพ แทนที่เมทริกซ์ด้วยจำนวนโหนดทั้งแนวตั้งและแนวนอน โดยกำหนดให้แนวนอนเป็นโหนดต้นทางและแนวตั้งเป็นโหนดปลายทาง สามารถเขียนเลขลำดับเมทริกซ์โดยระบุค่า ดังนี้
พิจารณาโหนด A มีเส้นเชื่อมต่อระบุไป B ระบุหมายเลย 1 นอกนั้นระบุค่าเป็น 0
พิจารณาโหนด B มีเส้นเชื่อมต่อระบุไป C, E ระบุหมายเลย 1 นอกนั้นระบุค่าเป็น 0
พิจารณาโหนด C มีเส้นเชื่อมต่อระบุไป D, E ระบุหมายเลย 1 นอกนั้นระบุค่าเป็น 0
พิจารณาโหนด D ไม่มีเส้นเชื่อมต่อไปยังโหนดอื่น B ระบุหมายเลข 0 ทุกช่อง
พิจารณาโหนด E มีเส้นเชื่อมต่อระบุไป D, F ระบุหมายเลย 1 นอกนั้นระบุค่าเป็น 0
พิจารณาโหนด F ไม่มีเส้นเชื่อมต่อไปยังโหนดอื่น B ระบุหมายเลข 0 ทุกช่อง
ไม่มีความคิดเห็น:
แสดงความคิดเห็น